Appendix C: Analytic Methods

SAMPLE (ANALYTIC) WEIGHTS

The survey sample was weighted to account for the differential probability of being sampled among strata, for nonresponse, and for respondent ineligibility. These statistical adjustments allow the analysis to properly infer back to the correct Gulf War population. The calculations were done as follows.

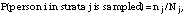
Respondents were randomly sampled within strata. For a predetermined number of respondents to be drawn from strata j, nj,

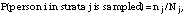
where Nj is the total number of persons in strata j in the sampling frame. In the absence of nonresponse and ineligibility issues, the weight for person i in strata j would simply be Wi = Nj/nj However, nonresponse and ineligibility affect nj and Nj, respectively, and they must be adjusted to arrive at weights that will allow proper inference back to the population of interest.

Nonresponse[1] was accounted for using the propensity score method of Little and Rubin (1987) to determine the probability that person i responds given that person i was sampled. This probability was calculated by fitting the logistic regression model

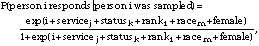
where i is the intercept coefficient and the other coefficients are the coefficients for indicator variables corresponding to person i's membership in various groups:

These factors were all found to be significant predictors of the probability of response: Individuals who were in the Air Force were more likely to respond than those in the other services; retired personnel were easier to locate than personnel still on active duty or in the reserves, and civilians were harder to locate; and minorities and females were less likely to respond. The model was fit to all persons in the sampling frame less the ineligibles.

From this, the probability that person i in strata j was sampled and responded, pr(i), was calculated as

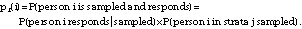
Similar to the propensity score model for nonresponse, strata sizes were adjusted for ineligibility using a logistic regression model. A model was fit that expressed the probability that a person listed in the Gulf War database was not in ODS/DS based on demographic characteristics. The model was fit to all survey respondents (the eligibles) versus those in the sampling frame who were reached but indicated that they had not served in ODS/DS (the ineligibles). The model is thus similar to the nonresponse model, although the covariates differed to reflect the dimensions important to ineligibility:

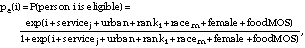
where, as before, i is the intercept coefficient and the other coefficients are the coefficients for indicator variables corresponding to person i's membership in the previously described groups (less status) plus:

Both "urban" and "foodMOS" are important predictors of eligibility as those persons were more likely to have been in ODS/DS. In particular, the urban indicator was generated for units known to be in the Gulf War, so personnel whom the database indicated were in these units were more likely to have been in ODS/DS.

To estimate the correct size of the strata, these probabilities were calculated for each of the 536,790 people in the Gulf War database and summed by strata. Thus

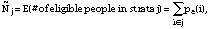
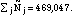so that the total number of personnel estimated to have been on the ground in-theater is estimated to be Using the adjusted strata sizes, the final analytic weights for each respondent were calculated as

BASIC ANALYTIC METHODOLOGY

In general, we used standard statistical techniques in our analysis. This section describes the methodology used to account for the stratified random sample and details of the models underlying the results in Tables 4.7 to 4.10.

Standard Error Calculations

In all of the statistical calculations, we used the linearization method (Skinner, Holt, and Smith, 1989) as implemented in the SUDAAN software (Shah, Barnwell, and Bieler, 1997) to account for the stratified sample in our estimates of standard errors.[2] The linearization method uses a first-order expansion to approximate via a weighted sum of random variables a nonlinear statistic. The variance of the nonlinear statistic is then estimated by the variance of the weighted sum, which is estimated using standard formulas for linear statistics. See Skinner, Holt, and Smith (1989) or Shah, Barnwell, and Bieler (1997) for complete details on this method.

Modeling Details

The results of Tables 4.9 and 4.10 are based on log-linear regression models. In particular, for respondents who indicated they used a particular form of pesticide, we modeled the log of the frequency of use as a linear function of various demographic covariates. The model is of the form

where Y is the frequency of use, and the Xs are covariates related to population demographics. The fitted model is then of the form

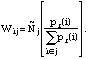
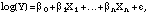
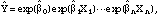
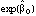where the Xs are indicator variables representing respondent membership in various demographic categories. Thus, can be interpreted as the average pesticide use for the baseline group, and 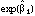can be expressed as the percentage change from the baseline rate for a member of the ith demographic group. The baseline group is defined as the group corresponding to having all the indicator Xs in the model set to zero.

Tables 4.7 and 4.8 are based on standard logistic regression models, using the whole respondent population, with a dependent variable that simply indicates whether each respondent said he or she used a particular pesticide form or not. In logistic regression, the log-odds is assumed to be a linear function of various covariates. Thus, the basic form of the model is

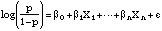
where p is the probability that a pesticide form was used.

This means that the odds, p/(1 - p), can be expressed as a multiplicative function of the fitted coefficients. Since the covariates in the model are all indicator functions for respondent membership in various demographic categories, the exponentiated coefficients can be expressed as the percentage change in the estimated baseline group's odds, .

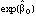The logistic regression results for PB pill usage presented in Chapter Five are based on a similar model--the dependent variable is whether a respondent took PB pills or not--with the same set of covariates.

Standard errors in both the linear and logistic regression models were adjusted for stratified sampling as discussed in the previous subsection.

IMPUTING ACTIVE INGREDIENTS IN PERSONAL-USE PESTICIDES

This section contains information on the process used to impute active ingredients for personal-use pesticides for Tables 3.10 to 3.12. The process was conducted in two main steps: (1) as much as possible, classify active ingredients directly from information given by respondents, and (2) for those that could not be directly classified, impute the probability of active ingredients.

Classification

There are two main classification problems, related to whether the respondent provided a product name or not. In either case, the goal is to try to determine the active ingredient using the information provided. When names were given, and the name was for a known pesticide, the determination of the active ingredient was straightforward. Respondents could also indicate "other" and provide a name not from the survey list. When such an "other" was provided, and when a name could not be remembered at all, the respondent was also prompted for the color, smell, and use of the pesticide. This information was then used to try to identify the active ingredient. Finally, if the pesticide was identified as military issue, but it could not be classified by name or by color/smell/use, then the form was matched to known military-issue pesticides.

When the active ingredient could not be uniquely determined from the information given, all possibilities were recorded. For example, a spray that smelled like insecticide that was used on the uniform could have had either permethrin or DEET as the active ingredient. In such a case, both possibilities were allowed. Then later, as discussed in the next section, the probabilities of whether the spray was permethrin or DEET were imputed from the distribution of uniquely identified active ingredients.

For unnamed products, it was assumed that the pesticide was appropriately used when classifying it. For example, sprays that were used on the body only are assumed to be DEET-based and not permethrin (which should have been used on uniforms).

If a pesticide name from the survey list was given, then the active ingredient was classified according to the "rules" listed in Table C.1.

Table C.1
Rules for Mapping Personal-Use Pesticide Products to Active Ingredients

Product Name Active Ingredient
DEET, Insect/Arthropod Repellent, Cutter Insect Repellent, Off, 3M Repellent, any Cutter personal products, 3M, Repellent DEET
Permenone; any combination and/or permutation of the following words: Wasp Freeze, Hornet Killer, Wasp Stopper, Raid Permethrin
Diazinon Dust, Diazinon 4E; Diazol Diazinon
6-12 Ethyl hexanediol
DDT DDT
Parathion Parathion
Chigg-Away Sulfur
Skin-So-Soft none

If an "other" name was provided, that name was first used to try to identify the active ingredient. Rules for this are listed in Table C.2.

Table C.2
Rules for Mapping Personal-Use Pesticide Products to Active Ingredients Given "Other" Names (Not Listed in the Survey)

If the "Other" Response Contained: Active Ingredient
DEET, Deep Woods, Off, Bug Juice, Bug Dope, Muskol DEET
Permenal, perminal, permithen, permithium, peramone, permenone Permethrin
6-12, 6-22 Ethyl hexanediol
Phenitrin, d�phen d-Phenothrin
DDT DDT
Parathion Parathion
Gig-away Sulfur
Hawaiian Tropic, Skintastic,a Soft Scent, Lubriderm None

aSkintastic, a product with pesticide ingredients, was not available in 1990-1991. We thus assumed that it was a nonpesticide commercial lotion.

For unnamed pesticides and those pesticides that could not be classified according to the "other" name given, the active ingredient was inferred from some combination of form, color, smell, and use. The rules for this classification are given in Table C.3.

Table C.3
Rules for Mapping Unnamed Personal-Use Pesticide Products, by Color, Smell, and Use to Active Ingredients

Form Color Smell Use Active Ingredient
Spray n/a Off, DEET, or sweet Any DEET
Spray n/a Raid Any Permethrin
Spray n/a Insecticide or chemical Body DEET
Spray n/a Insecticide or chemical Uniform or body and uniform DEET or permethrin
Powder White, cloudy, cream, yellow, or gray Insecticide, chemical, or musty Any Lindane
Liquid Clear Sweet, off Any DEET
Liquid White, clear, light brown, or yellow Sulfur Any Sulfur
Liquid White or yellow Insecticide or chemical Any Permethrin
Liquid Clear Insecticide or chemical Body DEET
Liquid Clear Insecticide or chemical Uniform or body and uniform DEET or permethrin
Lotion White, clear, light brown, or yellow Sulfur Any Sulfur
Lotion White, cloudy, cream, or clear Insecticide or chemical Any DEET
Stick or Wipe Any Any Any DEET, Ethyl hexanediol

In addition, for respondents reporting multiple smells, the smell response could not contain: alcohol, cooking oil, diesel, gasoline, kerosene, medicine, musky, petrol, or powder. The smells of musty and sulfur had to be alone to code to lindane or sulfur, respectively. And perfume alone did not code to any active ingredient.

If the active ingredient could not be classified via the rules in Tables C.2 and C.3, but a physical description of a military-issue container was provided, the rules in Table C.4 were used.

Table C.4
Rules for Mapping Personal-Use Pesticide Products, Where "Other" Response Reflected That the Pesticide Was Military Issue(and It Did Not Otherwise Classify)

If the "Other" Response Indicated The Pesticide Was Military Issue And It Met The Following Conditions:
Form Use Other Conditions Active Ingredient
Liquid or spray Body DEET
Liquid or spray Uniform or body and uniform DEET or Permethrin
Liquid Any Comments or smell field gave a sulfur smell Sulfur
Lotion Any Comments indicated a "tube" container DEET
Lotion Any Comments indicated a "bottle" or "green" container DEET
Powder Any Comments or smell field gave a musty smell Lindane

Finally, if only a subset of the information was given, say form and color but not smell, then the response was mapped to all possibilities with matching form and color. If color or smell did not map to those values in the table, it was treated as missing. In the most extreme case, if both smell and color were missing, then the response was mapped to all the active ingredients for that form (consistent with the reported use).

Imputation

Frequently, the classification scheme previously described resulted in multiple active ingredient possibilities. To calculate the personal pesticide usage by active ingredient in Tables 3.10 to 3.12, we imputed the fraction of the population exposed to each active ingredient. The calculations were conducted in three main steps: (1) The probability that a respondent used each active ingredient was estimated, (2) the frequency of use was combined and the fraction of the population for each frequency of use estimated, and (3) the variability of the various usage statistics was calculated.

Probability of Active Ingredient Estimation. To estimate the probability that a respondent used an active ingredient, we used a methodology motivated by the EM algorithm of Dempster, Laird, and Rubin (1977). Since the distribution of pesticides varied by demographic characteristics, personnel were grouped into similar cohorts to condition the calculations on those characteristics. Sprays and liquids were conditioned on service and usage (body, uniform, or body and uniform); all others were conditioned on service and gender.[3]

Let pd, pp, pb, and po be the unknown probability that a random individual in the cohort used the active ingredients DEET, permethrin, sulfur, and "other," respectively. For a given respondent in the cohort, let Id, Ip, Ib, and Io be indicators derived from the classification scheme for whether the respondent may have used each of the active ingredients.

For each cohort, the distribution of pesticide use was imputed as follows. First, all the uniquely identifiable pesticides were used to generate an initial estimate of the distribution on active ingredients. For a given cohort, this was estimated as

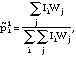
for all j in the cohort and where i = d, p, b, or o. Then, each individual's probability of using an active ingredient was estimated as

.

The cohort's overall probabilities and individual probabilities are then iteratively reestimated by alternating between

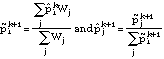
until

.

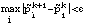
We ultimately used = 0.01 after empirically determining that the final result was insensitive to further reductions in .

Estimation of Frequency of Use. To estimate the frequency of use for each active ingredient by the fraction of the population represented by person i, it was necessary to combine the various frequencies of use between and within forms. For example, person i may have used two sprays and one liquid, each of which had some probability of being DEET and another probability of being permethrin, and each had a reported frequency of usage. Some individuals in Wi, the fraction of ODS/DS population represented by person i, may have used all DEET products, so that their DEET usage is the sum of the three use frequencies and their permethrin usage is zero. Others may have used all permethrin products and no DEET, and still others may have used some combination of active ingredients.

To estimate the fraction of each Wi that used a particular active ingredient with a particular frequency, we assumed that for each person the probability of using one product was independent of the probability of using another product. Each person could have reported using up to nine personal products (three sprays, three liquids, and three lotions) that could have contained the active ingredients of interest (DEET, permethrin, and sulfur). Each product reported had a frequency of use and an imputed probability distribution on the three possible active ingredients and "other nonpesticide."[4] For each person, let fij be the reported frequency of use for product j, j = 1, . . . 9. Let pijk be the imputed probability that product j has active ingredient k. Finally, let Ij be an indicator variable for product j and let the group of nine indicators I form a column vector. There are 2(9-1) = 511 possible vectors for which at least one indicator is nonzero. Each vector represents a combination of products that might have contained a particular active ingredient.

Then, for each indicator vector, we calculated

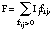
and for each F > 0 we then calculated

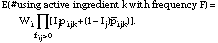
The result is that each survey respondent's weight, Wi, is apportioned by active ingredient and frequency of use within active ingredient.

Estimation of Standard Errors. To capture the uncertainty resulting from the imputation of active ingredients, we used the Bootstrap (Efron and Tibshirani, 1993) to calculate standard errors. For a given statistic, say the mean frequency of usage of an active ingredient, its standard error is calculated as follows. Let 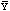be the mean frequency of usage calculated. Then the Bootstrap proceeds to resample with replacement from the original observations. Because this was a stratified random sample, the resampling was done with replacement within strata, maintaining the total number of resampled observations within each stratum equal to the original number of respondents in each stratum. After each resample was drawn, the entire imputation was redone, and a new bootstrap statistic, 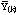, was calculated, k = 1, . . . ,M. From these bootstrap statistics 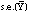is estimated as

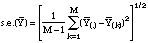
where

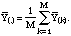
We ultimately used M = 200 in the calculations, consistent with what is normally recommended (Efron and Tibshirani, 1993), as our results differed insignificantly for M = 400.

[1]"Nonresponse" as used in this appendix includes those who refused to participate and those who were not located--essentially everyone in the sampling frame who did not complete the survey, minus those who were ineligible.

[2]Except for the imputation of personal-use active ingredients in Tables 3.10 to 3.12, as described in the next section.

[3]Additional conditioning was not possible of because small cell sizes.

[4]Although the survey asked only about pesticides, respondents sometimes reported nonpesticides. Thus, to avoid bias in the imputation, we also imputed from the nonpesticides and estimated a probability that a product was not a pesticide.

Contents
Appendix B
Appendix D