1. Data Acquisition
Acquiring meteorological data is a major element of the reconstruction effort. The modeling teams collected conventional (non-satellite) observational data archived at the National Climatic Data Center, National Center for Atmospheric Research (NCAR), NRL, and FNMOC, along with satellite observational data from NOAA and the Defense Meteorological Satellite Program (DMSP). These data, discussed below, included the operational set assimilated into the forecast analyses produced by operational weather centers in March 1991, as well as the since-declassified observations described above.
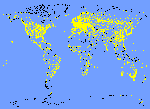
a. Surface Observations. Surface stations are distributed irregularly over land and along main shipping routes over the globe (Figure A-8). Surface observations, taken at 1- to 3-hour intervals, include pressure, temperature, wind components, and relative humidity. Typical errors associated with surface observations are 0.5 mb for surface pressure, 1� K for temperature, 3 m/s for the wind, and 10% for relative humidity. Surface wind observations over land may reflect local, topographically-forced features with spatial and temporal scales much different from the observational network. Navy ships reported surface observations over water throughout the Persian Gulf area (Figure A-9) during March 10-14, 1991, but were not received at the weather centers for the 1200 UTC assimilation for March 10, 1991. However, the NOGAPS reanalysis and all mesoscale forecasts and analyses incorporated the late-arriving data. Mobile USAF special operations teams reported surface observations in Iraq (Figure A-6) during March 10-14, 1991. The 1997 Khamisiyah analysis did not substantially include these data. (NRL and NCAR did not assimilate these observations; DTRA assimilated them in the OMEGA objective analysis but with diminished weight.)
Figure A-8. Locations of global network of regular surface observations
b. Upper-Air Data. NCDC receives and maintains rawinsonde upper air observations (observation locations shown in Figure A-10), pilot balloon (pibal) observations (observation locations shown in Figure A-11), and aircraft reports. Closed symbols in Figures A-10 and A-11 represent data available only through classified networks to military sites during the Gulf War. Variables recorded by rawinsondes include temperature, pressure, humidity, and wind components at 12-hour intervals. Pilot balloons observe wind only. The typical errors for upper-air observations are 1 K in temperature, 3-5 m/s in wind, and 10% in relative humidity. Wind errors tend to be larger at higher elevations. Operational data reported promptly to the WMO in March 1991 did not include rawinsonde observations from Saudi Arabian stations near its border with Iraq, because Saudi Arabia feared Iraq might decide to launch chemical weapons based on the data. These data, along with since-declassified Navy data, were included in the 1999 Khamisiyah reanalysis.
Figure A-10. Locations of Naval Research Laboratory's March 10-14, 1991, rawinsonde observations
Figure A-11. Locations of Naval Research Laboratory's March 10-14. 1991, pibal observations
c. Satellite Observations. WMO does not consider satellite data part of the conventional data set. Polar-orbiting satellites containing radiometers take vertical soundings of air temperature. Satellites observe radiance on several spectral channels and use inversion algorithms to convert the measurements to temperature. The coverage is global but the reports tend to follow the satellite orbits. Figure A-12 shows the pattern of geosynchronous satellite retrievals. The observations represent an average over areas ranging in size from 10 to 200 km. The vertical resolution is coarse, about 200 millibars (mb) in depth. These observations are more reliable in clear rather than cloudy skies. Geosynchronous satellites observe cloud drift winds—at both high (200mb) and low (850mb) levels—from sequences of cloud photographs (Figure A-13). Image sequences allow the tracking of individual cloud elements to estimate wind speed and direction. This technique has several difficulties, particularly in determining the altitude and speed of the tracked cloud element, because clouds do not necessarily move at the speed of the wind.
Figure A-12. Locations of global network of polar-orbiting satellite retrievals
Figure A-13. Locations of global network of geosynchronous satellites' cloud tracking retrievals
d. Surface Characteristic Databases. In addition to observed values of atmospheric conditions (e.g., wind speed and direction and thermodynamic variables), surface characteristic databases also are necessary to predict surface-driven mesoscale circulations. Warner and Sheu (2000) show subtle differences in land use can significantly affect the model-predicted PBL structure. These databases provide detailed information on surface parameters (such as land and water distribution, terrain elevation, surface roughness, soil type, climatological vegetation index, albedo, sea and land temperatures, and land use and cover.) These parameters are used to determine temperature, moisture, and wind profiles in the surface layer. All three mesoscale models predict soil temperature and ground wetness as time-dependent variables. These surface parameters’ spatial resolutions vary with the mesoscale models’ configurations. At the time of the COAMPS reanalysis (March 1997), FNMOC global data sets exhibited a resolution of approximately 1� longitude and latitude. NCAR currently uses the US Geological Survey (USGS) global data set obtained from satellite imagery, which has a spatial resolution of 1 km. DTRA has configured OMEGA to assimilate data from eight types of surface characteristic databases ranging from 1� global soil type data to 2 minute land use, cover, and vegetation data. For both vegetation index and land cover, two different data sets are available. The 2 minute data set covers North America only at high resolution; the other covers the entire globe, but at lower resolution. Both MM5 and OMEGA used coarse-resolution surface data for the 1997 Khamisiyah analysis. Figure A-14 shows an example of the land-use category MM5 used.
Figure A-14. Land-use categories used by MM5
e. Gridded Global Analysis. Global gridded analysis fields are necessary to provide (1) background fields for initializing a mesoscale analysis cycle and (2) large-scale information for interpolations at the mesoscale models’ lateral boundaries.
To provide appropriate large-scale data to reconstruct mesoscale meteorology, the operational weather centers used several global gridded fields. These centers, including NCEP, NCAR, the National Meteorological Center, ECMWF, and FNMOC, maintain a suite of numerical forecast models, both global and mesoscale. Various sites store the analysis fields that these operational models produced in March 1991.
Recent projects by NCEP and NCAR (Kalnay et al., 1996) and ECMWF (Gibson et al., 1997) have produced reanalyses of global weather over multi-decade periods, including March 1991. These projects seek to improve the global analysis data sets’ accuracy and consistency by reproducing them with state-of-the-art data assimilation and forecast systems while also enhancing the set of assimilated land surface, ship, rawinsonde, pibal, aircraft, satellite, and other data. During 1996 to 1997, NCAR and NCEP reanalyzed the time period 1958-1993 to take advantage of improvements in NCEP’s model resolution (Spectral T62, about 210 km in horizontal resolution, and 28 vertical hybrid levels) and the parameterization of physical processes. NCEP and NCAR’s reanalysis data are available at a 2.5� horizontal resolution and at 17 pressure levels. The ECMWF global reanalysis (1979-1993) included full model resolution analyses (Spectral T106/Gaussian N80, about 1.125� in horizontal resolution, and 31 vertical hybrid levels). The data are available at a reduced resolution (2.5� , 17 pressure levels, 6-hour intervals). Although it is likely the NCEP-NCAR and ECMWF reanalyses assimilated the delayed March 1991 Saudi Arabian observations, it is unlikely these reanalyses included declassified Navy ship data. To provide the COAMPS initialization and lateral boundary conditions from its compatible global model, NRL performed a new global weather reanalysis for December 1990 through March 1991 using the NOGAPS global atmospheric data assimilation and forecast model, with a 6-hour data assimilation cycle and a 0.75� horizontal resolution. The NOGAPS reanalysis used all the meteorological data cited above, including the delayed and declassified field data.
2. Data Assimilation
Once the above data are acquired, they are assimilated into model predictions. Model assimilation typically contains these four components (Daley, 1991).
a. Quality Control. Quality control algorithms are designed to modify and reject erroneous meteorological data occurring either naturally or through gross errors. Natural errors include limits to instrument accuracy and deviations caused by small-scale perturbations of meteorological fields at the observing site. Gross errors originate from improperly calibrated or malfunctioning instruments, incorrect registration of observations, incorrect coding of observations, and telecommunication errors. Both natural and gross errors can be either random or spatially or temporally correlated. Improper calibration of observing instruments can result in systematic biases.
Quality control techniques include checks for duplicate reports, plausibility (e.g. above-freezing at 300mb), and contradictions, based on an analysis of two or more parameters at the same point (e.g., occurrence of rain in the absence of clouds). Other procedures may apply consistency checks, such as temporal continuity with past observations, or dynamic balances, such as geostrophic and hydrostatic.
For the Khamisiyah analysis, NCAR implemented a manual quality contol system in which they checked the observations against a Cressman-type (Cressman, 1959) analysis that synthesized the ECMWF reanalysis fields and conventional observational set archived at NCAR.
b. Objective Analysis. Numerical weather forecasts require the specification of meteorological variables at the beginning of the forecast periods to provide the initial state from which the models can integrate the system of differential equations forward in time. To reconcile observations defined at arbitrary locations with initial gridded fields, analysis methods such as optimum interpolation were developed. These methods are applicable to both mesoscale and global forecast models. The models then integrate the reconciled data forward in time on a computational grid based on the dynamic laws of physics. These objective analysis methods are applied to the problems of initializing and merging new observational data with the continuing model integration (Dynamic Data Assimilation or DDA). Daley (1991) describes objective analysis in detail.
c. Initialization. The objective analysis methods described previously do not generally provide an initial balance in mass and wind fields. These imbalances in initial data excite spurious inertia-gravity wave oscillations constituting meteorological noise. Left unchecked, these high-frequency gravity-wave oscillations can grow in amplitude and obscure slower-moving meteorological signals. To eliminate or attenuate these waves at initialization, a standard approach applied in most global-scale models consists of projecting the disturbance on the subspace orthogonal to the normal modes of the dynamical equations. NOGAPS and the ECMWF and NCEP models use the nonlinear normal mode initialization, which reduces the directional tendency of the unwanted modes, rather than their amplitude. Although appropriate for intermittent DDA, it should be noted normal mode initialization is a distinct step from objective analysis and, hence, usually changes the analysis fields such that they may no longer fit the observations as closely.
Initialization in mesoscale models differs from that in global-scale models. On the one hand any large imbalance in the initial condition must be eliminated, while on the other hand, mesoscale details must be preserved. For example, in the COAMPS 1999 reanalysis for the Khamisiyah release, NRL used previous forecasts as the first-guess fields, so there is no large imbalance (the only balance imposed is that the vertical perturbation pressure gradient be in hydrostatic balance with the buoyancy term in the vertical equation of motion), except possibly at the cold start (i.e., when the model is first initialized.) Therefore, the cold start time was pushed as early as feasible. OMEGA and MM5 do not apply an explicit initialization step because their analysis schemes leave only minimal imbalances.
d. Dynamic Data Assimilation. Dynamic data assimilation is a method in which the growth of errors in a dynamic model forecast is checked by incorporating observations corresponding to times after the model’s initialization time. Models employing DDA can use observations of a variable throughout an integration period, instead of using observations only at initialization. Fast (1995) showed DDA effectively reduces accumulated errors found in dynamic models, especially for simulation periods longer than 48 hours. Seaman (1997) has suggested that care must be taken when developing a strategy to insert and weight data into a model integration. The data should be weighted such that its area of influence is consistent with the dominant spatial scales present in the atmosphere.
There are two major forms of dynamic data assimilation (Seaman, 1997): intermittent and continuous.
1) Intermittent Assimilation. Intermittent methods stop the model at regular intervals (i.e., at analysis times) during the numerical integration, use the model fields at those times as a first guess for a new objective analysis (which accounts for the updated observations), and use the resulting analysis fields to restart the model for the next integration interval. Global models and some mesoscale models extensively use these methods. Figure A-15 represents the four steps repeated at each assimilation cycle (typically 6 hours for global and 12 hours for mesoscale systems). After using quality control algorithms to check the observational data, the observations and a first-guess field are used to perform a three-dimensional optimal analysis. The first-guess field is a previous model forecast valid at the analysis time. For global models, analyzed fields are further adjusted by an initialization scheme that attenuates the fastest-moving waves. No such explicit initialization scheme is applied in a mesoscale assimilation cycle. Intermittent updating takes advantage of observational data that becomes available at standard intervals, e.g., 0000 UTC and 1200 UTC. Each restart incorporates fresh data to limit error growth, but also can cause spin-up error due to imbalances in the reinitialized fields. NRL currently uses a digital filter algorithm to reduce the errors.
Figure A-15. Four step assimilation cycle
2) Continuous Assimilation. MM5 implements another method of dynamic assimilation that incorporates observational data into the forecasts at every time step between the previous analysis step and the observation time, thereby minimizing spin-up error. Dynamic assimilation uses the nudging or Newtonian relaxation technique to relax the model state toward the observed state (at the next model time) by adding extra forcing terms (based on the difference between the two states) to the governing equations. As a result, the model fields gradually correct themselves, requiring no further dynamic balancing through initialization. Typically, the magnitude of the nudging term is constrained and small compared to the major physical terms in the dynamic equations, except for brief periods that may require significant correction to the model solution.
3. Mesoscale Forecasts
As pointed out by numerous authors, the resolution of the available meteorological data primarily affects the predictive success of dispersion models (Draxler, 1992). Neither the observational network (spatial resolution of the upper-air sounding stations is 300-500 km; temporal resolution is 12 hours) nor gridded global analysis fields sufficiently resolve wind fields to support detailed boundary-layer transport calculations. Hazardous dispersion modeling of near-surface releases requires adequately resolving the planetary boundary layer to ensure sufficient accuracy in the prediction of the contaminant plume characteristics. For example, detailed boundary layer resolution is essential when representing differential heating along complex terrain and across land-water boundaries, since significant vertical gradients of the meteorological variables can occur within the PBL (Anthes et al., 1980). The use of high-resolution land use databases requires the application of non-hydrostatic models capable of resolving the forced modes generated by spatially-inhomogeneous surface characteristics. As a result, a comprehensive meteorological reanalysis of the Khamisiyah scenario requires a mesoscale prognostic model based on non-hydrostatic equations. A non-hydrostatic model is appropriate when the horizontal spatial scale of the mesoscale disturbance is comparable to the density scale height of the atmosphere (~ 8 km).
High resolution, mesoscale forecasting systems are characterized by many specific model features, including non-hydrostatic, quasi-compressible primitive equations; terrain-following coordinate systems; nested or adaptive grid structures; high-resolution turbulence and planetary boundary layer parameterization; microphysics; short- and long-wave radiation; prognostic soil-layer moisture and temperature models; vegetation parameterization; numerical procedures capable of eliminating rapidly propagating sound waves; and initialization based on large-scale model analyses or forecasts and observations. Numerous references discuss in detail these topics related to mesoscale meteorological models (e.g., Pielke, 1984; Cotton and Anthes, 1984).
C. Reconstructing Dispersion Patterns Via Dispersion And Transport Modeling[9]
Atmospheric dispersion models play a principal role in reconstructing the Khamisiyah release. These models calculate the transport, turbulent diffusion, decay, and deposition of a chemical warfare agent released into the atmosphere and estimate the concentration of the released agent and the resulting dosage (concentration integrated with time) as a function of location and time. Information obtained from atmospheric dispersion models forms the basis for epidemiological studies that will explore the possible impact of the Khamisiyah Pit release on US military units. For this process, DoD has adopted HPAC/SCIPUFF and VLSTRACK, the two primary hazard prediction models endorsed in the Office of the Assistant to the Secretary of Defense for Nuclear and Chemical and Biological Defense Programs (OATSDNCB) memorandum (1996).
The primary
variable of interest in most dispersion studies is the ensemble mean concentration 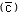 .
Because of turbulent motions of different scales in the atmosphere, the instantaneous
concentration field fluctuates around the ensemble mean concentration. Although
the theory of ensemble mean concentrations is fairly well established and defines
the output from most operational hazard prediction models, this theory addresses
only one aspect of the turbulent diffusion process: the first moment of the
probability distribution of the random variable, concentration. Typically, concentration
fluctuations (s c)
are in the same order of magnitude as the mean concentration and, hence, the
second moment of the probability distribution is of significance. The probability
distribution function (PDF) provides the statistical description of characteristic
fluctuations. Commonly assumed PDFs include log-normal and clipped normal (Yee
and Bowers, 1990). Note that the ratio of s c
to
.
Because of turbulent motions of different scales in the atmosphere, the instantaneous
concentration field fluctuates around the ensemble mean concentration. Although
the theory of ensemble mean concentrations is fairly well established and defines
the output from most operational hazard prediction models, this theory addresses
only one aspect of the turbulent diffusion process: the first moment of the
probability distribution of the random variable, concentration. Typically, concentration
fluctuations (s c)
are in the same order of magnitude as the mean concentration and, hence, the
second moment of the probability distribution is of significance. The probability
distribution function (PDF) provides the statistical description of characteristic
fluctuations. Commonly assumed PDFs include log-normal and clipped normal (Yee
and Bowers, 1990). Note that the ratio of s c
to 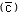 depends on the averaging time; thus, s c
decreases as averaging time increases. For chemical agents, where dosages are
more important that concentrations, the averaging time is relatively large and
s c may be small.
depends on the averaging time; thus, s c
decreases as averaging time increases. For chemical agents, where dosages are
more important that concentrations, the averaging time is relatively large and
s c may be small.
1. Model Approaches. There are two basic approaches to modeling atmospheric dispersion. The first approach is Eulerian, which describes the behavior of pollutants relative to a fixed coordinate system. The second approach is Lagrangian, which describes concentration changes relative to a moving frame of reference. Arya (1999) describes the two approaches in detail. Both HPAC/SCIPUFF and VLSTRACK are based on the Lagrangian approach.
2. Source Representation and Parameterizations. DoD and CIA assumed the Khamisiyah Pit release of agent consisted of: (1) aerosolized liquid droplets and vapor produced by the normal action of a bursting rocket (burster-tube detonation), (2) explosive, catastrophic rupture of one or more containers by either demolition blast or secondary hydraulic rupture from physical impact, (3) spilled liquid from damage to the container (leaking over minutes or as much as an hour), and (4) open containers without major spillage (slow evaporation of liquid over several days). Quantifying these processes required material-specific evaporation tests and samples of barren, desert soil and wood samples consistent with the Khamisiyah rocket crates.
The initial agent characteristics depend on the physical properties of the destroyed munition (i.e., the quantity, munition type, agent fill, etc.), demolition method, and the interaction of the disseminated agent with the local meteorological conditions immediately after the release. The munition type is well known to be 122mm rockets, and the May 1997 Dugway field tests established the likely characteristics of the rockets’ detonations.
For the purposes of event reconstruction, DoD and CIA considered two primary approaches when designing the Dugway field tests. The first approach intended the field trials to generate basic information, such as the initial breakdown of the release into different pathways (e.g., instant vaporization versus spillage onto wood and soil) to specify the total agent mass released or evaporated as a function of time, described in Appendix A, Section IV.B.1. Models such as VLSTRACK and HPAC/SCIPUFF are configured to use the externally specified source term, but their internal source calculations were not used due to the uniqueness of the Khamisiyah Pit event.
a. Evaporation. In a standard chemical warfare agent attack, after the initial release, the contaminant cloud, made up of liquid droplets, falls due to gravitational settling and moves downwind, transported by the local flow field. During this settling and transport, the liquid droplets may evaporate depending on local meteorological conditions. Since the demolition techniques applied at Khamisiyah most likely failed to trigger most rockets’ central burster tubes, the agent released there was unlikely to follow the standard chemical warfare agent-dispersion scenario. More likely, the ruptured warheads spilled pools of liquid agent onto the sandy soil (which absorbed it) and onto the wood crating (which likely became saturated with the liquid agent, leading to evaporation). The Dugway and Edgewood evaporation tests, described in Appendix A, Section IV.B.1, were designed to quantify the evaporation rates for the Khamisiyah Pit release.
b. Decay. Chemical transformation phenomena is usually accounted for by assuming an exponential decay rate that is inverse of a time constant Tc, that can be time dependent per se:
|
|
(Equation
A-1)
|
|
|
|
The decay rate can include a diurnal variation, so the effects depending on solar radiation should be described. A recent review of the gas phase G-agent degradation literature identified two principal mechanisms for reducing sarin (GB) and cyclosarin (GF) vapor concentrations in the atmosphere: (1) the chemical reaction of the vapor with hydroxyl (OH) radicals during the day and (2) the chemical reaction of the vapor with nitrate (NO3) radicals during the night. (See TAB A-I.)
c. Deposition. Dry gaseous deposition refers to non-gravitational surface processes that transfer suspended material to available surfaces where the material is removed. The surface deposition rate depends on the contaminant’s material properties, the character of the surface, and the local meteorology.
For the Khamisiyah release, which is modeled as vapor, dry gaseous deposition at the surface is the primary mechanism for removing agent from the atmosphere. An empirical parameter called the deposition velocity typically characterizes the deposition rate:
|
|
(Equation
A-2)
|
|
|
|
Dry gaseous deposition can be modeled as involving three successive processes.
The first involves the transfer of material through the lower atmosphere to
the immediate vicinity of the surface. This is controlled by turbulent diffusion
in the atmospheric surface layer and is referred to as the aerodynamic component
of the transfer. The second involves the transfer of material across the thin
layers of air immediately adjacent to the elements that comprise the surface.
The net consequence of transfer across these layers of molecular exchange is
called the quasi-laminar layer resistance, reflecting the reality that it is
not precisely a laminar sublayer resistance by the net consequence of many of
these, each associated with some part of surface itself (e.g., leaves, twigs,
or grains of sand.) The third component is driven by the chemistry and biology
of the surface. It describes the net overall ability of the surface to capture
any molecule of material in question when it comes in contact. Following Wesely
and Hicks (1977), the deposition velocity, Vd, may be formulated
in terms of the specific transfer processes described above. In particular,
each layer may be represented as a region of resistance, and Vd is
calculated by
|
(Equation
A-3)
|
|
|
|
Several methods are available to incorporate dry deposition into dispersion models, including a source depletion model (Horst, 1979) that accounts for the loss of airborne material due to deposition by appropriately reducing the source strength as a function of downward distance, and a partial reflection model reported by Overcamp (1976).
| First Page | Prev Page
| Next Page |